November 20, 2013

Getting a fair result with an unfair coin

How can you get a fair coin toss if someone hands you a coin that is weighted to come up heads more often than tails?

Solution

This is @luismartingil solution. Please check all the Python source code here. This solution uses matplotlib for the plots.

We can have two different types of results when throwing the coin: {heads, tails}
We are going to have two players playing the game: {player-heads, player-tails}
player-heads is the player that chooses heads. player-tails the one choosing tails.
A fair game means that both players have the same probability of winning (50%).

We first need to know how unfair the game is in order to make it fair. We have to know how many times the coin comes up heads vs the times it comes up tails. We do this throwing the coin N times, where N is a huge number. After doing this we have a percentage of the times the coin comes up heads, lets call it p1. We can define the percentage of times the coin comes up tails as p2.

Based on the problem: - p1 and p2 are in this range [0, 100] - p1 will be bigger than p2. p1 > p2

We can assume that p2 = 100 - p1.

In order the game to be fair, player-heads has to win more than the p1 times of the times played in order to win the game. The bigger N is, the fairer the game is.

Proving the solution

Always back what you are saying!. A neat way to back my solution is to write some code and perform a simulation. That’s what I did.

Game simulation

 1 class Game(object):
 2     coin = None
 3     simulation = None
 4     def __init__(self, c):
 5         self.coin = c
 6     def simulate(self, n):
 7         self.simulation = {HEADS : 0, TAILS : 0}
 8         for i in range(n):
 9             self.simulation[self.coin.throw()] += 1
10         return self.whoWon()
11     def whoWon(self):
12         if self.simulation:
13             # PLAY_TAILS wins in case of even
14             return self.simulation, PLAY_HEADS if self.getCondHeads() else PLAY_TAILS

UnfairGame

Original game. It doesn’t know if the coin is weighted or not.

1 class UnfairGame(Game):
2     def getCondHeads(self):
3         return self.simulation[HEADS] > self.simulation[TAILS]

FairGame

A handicap is applied to the player-tails. Takes into account thw weight of the coin (coin.getPercent()).

1 class FairGame(Game):
2     def getCondHeads(self):
3         # PLAY_HEADS needs to win more to win the game. Handicap ;-)
4         # @luismartingil solution to the problem.
5         total = self.simulation[HEADS] + self.simulation[TAILS]
6         return (self.simulation[HEADS] > (self.coin.getPercent() * total))

Coins

Both FairGame and UnfairGame will be played with different coins.

Coin 1) 50% - 50%

Coin 2) 60% - 40%

Coin 3) 80% - 20%

Some plots. Playing the games

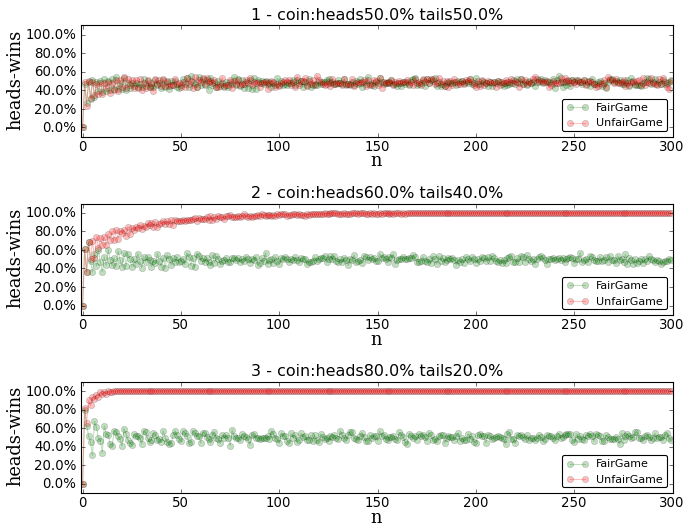
Plots-1, Player heads wins

These plots contains information about the wins of the player-head in a percentage based. Whether we have a fair or unfair {game, coin} the goal for a fair game is to see the points right in the 50% horizontal line, which would be the fairest game possible.

Some comments,

Coin 1). It doen’t matter which game we play using a fair coin (50% - 50%). It is always fair.
Coin 2-3). UnfairGame is always a looser game for player-tails using unweighted coin. This means that player-tails is likely to win in the beginning, but if he plays a bunch of times he will loose.
Coin 2-3). The more unweight is the coin, the faster it will converge.
Coin 2-3). Our FairGame solution works, it converges to 50% in all the cases.

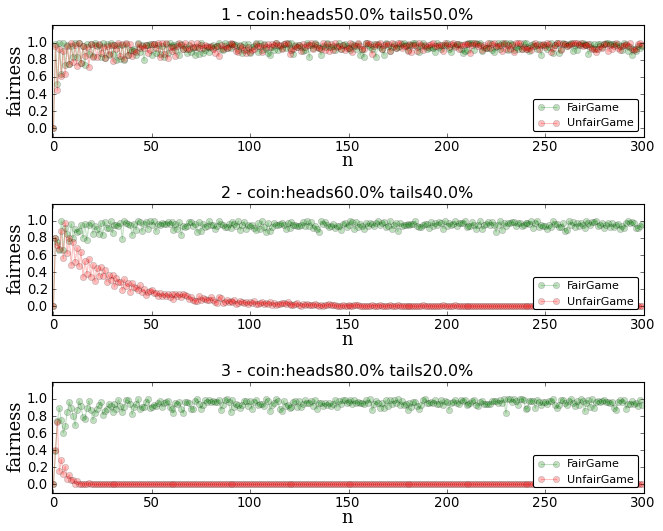
Plots-2, Fairness ratio : How fair is this solution?

I was curious about the fact of grading a fair solution. I came up with a function which returns how fair the solution is based on how close it is from the 50% percent. You can see the code and some plots below.

 1 def processFairness(percent):
 2     """ Return a value in [0, 1] defining how fair is the percent.
 3     0, worst.
 4     1, best.
 5     
 6     Applies the fairness function based on:
 7     if x == 50 , y = 1
 8     if 0 <= x < 50, y = x/50.0
 9     if 50 < x <= 100, y=-x/50.0 + 2
10     
11     |
12     |      (50,1)
13     |         _
14     |        /|\
15     |       / | \
16     |      /  |  \
17     |     /   |   \
18     |    /    |    \
19     |   /     |     \
20     |  /      |      \
21     | /       |       \
22     |/        |        \
23     ---------------------------------------------------------------
24     (0,0)   (50,0)   (100,0)
25     
26     """
27     if (percent == 50): ret = 1.0
28     elif (0 <= percent < 50): ret = float(percent) / 50.0
29     elif (50 < percent <= 100): ret = (float(-percent) / 50.0) + 2.0
30     else: raise percentOutOfRange('Error calculating fairness. percent:%s' % percent)
31     return ret